Please
Do Not Use This Reference Material WORD FOR WORD View Terms Of usage policy Page of this site for more Info on how to use this site.
Title: Simple Pendulum
Aim:
Apparatus: See your laboratory manual
Please
Do Not Use This Reference Material WORD FOR WORD View Terms Of usage policy Page of this site for more Info on how to use this site.
THEORY:
A pendulum is a weight suspended from a pivot so
that it can swing freely. When a pendulum is displaced sideways from its
resting equilibrium position, it is subject to a restoring force due to gravity
that will accelerate it back toward the equilibrium position. When released,
the restoring force combined with the pendulum's mass causes it to oscillate
about the equilibrium position, swinging back and forth. The time for one
complete cycle, a left swing and a right swing, is called the period. The
period depends on the length of the pendulum, and also to a slight degree on
the amplitude, the width of the pendulum's swing.
THEORY 1
The period of swing of a simple gravity pendulum
depends on its length, the local strength of gravity, and to a small extent on
the maximum angle that the pendulum swings away from vertical, θ0,
called the amplitude. It is independent of the mass of the bob. If the
amplitude is limited to small swings, the period T of a
simple pendulum, the time taken for a complete cycle, is:
where L
is the length of the pendulum and g is the local acceleration of
gravity.
For small swings the period of swing is
approximately the same for different size swings: that is, the period is
independent of amplitude. This property, called isochronism, is the reason
pendulums are so useful for timekeeping. Successive swings of the pendulum,
even if changing in amplitude, take the same amount of time.
For larger amplitudes, the period increases
gradually with amplitude so it is longer than given by equation (1). For
example, at an amplitude of θ0 = 23° it is 1% larger than
given by (1). The period increases asymptotically (to infinity) as θ0
approaches 180°, because the value θ0 = 180° is an unstable
equilibrium point for the pendulum. The true period of an ideal simple gravity
pendulum can be written in several different forms (see Pendulum (mathematics)
), one example being the infinite series:
The difference between this true period and the
period for small swings (1) above is called the circular error. In the
case of a typical grandfather clock whose pendulum has a swing of 6° and thus
an amplitude of 3° (0.05 radians), the difference between the true period
and the small angle approximation (1) amounts to about 15 seconds per day .
For small swings the pendulum approximates a
harmonic oscillator, and its motion as a function of time, t, is approximately
simple harmonic motion:[5]
For real pendulums, corrections to the period may
be needed to take into account the presence of air, the mass of the string, the
size and shape of the bob and how it is attached to the string, flexibility and
stretching of the string, motion of the support, and local gravitational
gradients.
THEORY
2
The kinetic energy
possessed by an object is the energy it possesses due to its motion. It is a
quantity that depends upon both mass and speed. The equation that relates
kinetic energy (KE) to mass (m) and speed (v) is
KE = ½mv2
The faster
an object moves, the more kinetic energy that it will possess. We can combine
this concept with the discussion above about how speed changes during the
course of motion. This blending of concepts would lead us to conclude that the
kinetic energy of the pendulum bob increases as the bob approaches the
equilibrium position. And the kinetic energy decreases as the bob moves further
away from the equilibrium position.
The potential energy
possessed by an object is the stored energy of position. Two types of potential
energy are discussed in The Physics Classroom Tutorial - gravitational
potential energy and elastic potential energy. Elastic potential energy is only
present when a spring (or other elastic medium) is compressed or stretched. A
simple pendulum does not consist of a spring. The form of potential energy
possessed by a pendulum bob is gravitational potential energy. The amount of gravitational
potential energy is dependent upon the mass (m) of the object and the height
(h) of the object. The equation for gravitational potential energy (PE) is
PE = mgh
where g
represents the gravitational field strength (sometimes referred to as the
acceleration caused by gravity) and has the value of 9.8 N/kg.
The height of an object is expressed relative
to some arbitrarily assigned zero level. In other words, the height must
be measured as a vertical distance above some reference position. For a
pendulum bob, it is customary to call the lowest position the reference
position or the zero level. So when the bob is at the equilibrium position (the
lowest position), its height is zero and its potential energy is 0 J. As the
pendulum bob does the back and forth, there are times during which the
bob is moving away from the equilibrium position. As it does, its height is
increasing as it moves further and further away. It reaches a maximum height as
it reaches the position of maximum displacement from the equilibrium position.
As the bob moves towards its equilibrium position, it decreases its height and
decreases its potential energy.
Now let's put these two concepts of kinetic
energy and potential energy together as we consider the motion of a pendulum
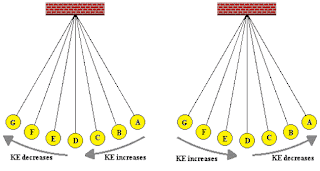
bob moving along the arc shown in the diagram at the right. We will use an energy bar chart
to represent the changes in the two forms of energy. The amount of each form of
energy is represented by a bar. The height of the bar is proportional to the
amount of that form of energy. In addition to the potential energy (PE) bar and
kinetic energy (KE) bar, there is a third bar labelled TME. The TME bar
represents the total amount of mechanical energy possessed by the pendulum bob.
The total mechanical energy
is simply the sum of the two forms of energy – kinetic plus potential energy.
Take some time to inspect the bar charts shown below for positions A, B, D, F
and G. What do you notice?
When you inspect the bar charts, it is evident
that as the bob moves from A to D, the kinetic energy is increasing and the
potential energy is decreasing. However, the total amount of these two forms of
energy is remaining constant. Whatever potential energy is lost in going from
position A to position D appears as kinetic energy. There is a transformation
of potential energy into kinetic energy as the bob moves from position A to
position D. Yet the total mechanical energy remains constant. We would say that
mechanical energy is conserved. As the bob moves past position D towards
position G, the opposite is observed. Kinetic energy decreases as the bob moves
rightward and (more importantly) upward toward position G. There is an increase
in potential energy to accompany this decrease in kinetic energy. Energy is
being transformed from kinetic form into potential form. Yet, as illustrated by
the TME bar, the total amount of mechanical energy is conserved. This very
principle of energy conservation was explained in the Energy chapter
of The Physics Classroom Tutorial.
Our final discussion will pertain to the period of
the pendulum. As discussed previously in this lesson,
the period is the time it takes for a vibrating object to complete its cycle.
In the case of pendulum, it is the time for the pendulum to start at one extreme,
travel to the opposite extreme, and then return to the original
location. Here we will be interested in the question ‘What variables affect
the period of a pendulum?’ We will concern ourselves with possible
variables. The variables are the mass of the pendulum bob, the length of the
string on which it hangs, and the angular displacement. The angular
displacement or arc angle is the angle that the string makes with the
vertical when released from rest. These three variables and their effect on the
period are easily studied and are often the focus of a physics lab in an
introductory physics class. The data table below provides representative data
for such a study.
Trial
|
Mass (kg)
|
Length (m)
|
Arc Angle (°)
|
Period (s)
|
1
|
0.02-
|
0.40
|
15.0
|
1.25
|
2
|
0.050
|
0.40
|
15.0
|
1.29
|
3
|
0.100
|
0.40
|
15.0
|
1.28
|
4
|
0.200
|
0.40
|
15.0
|
1.24
|
5
|
0.500
|
0.40
|
15.0
|
1.26
|
6
|
0.200
|
0.60
|
15.0
|
1.56
|
7
|
0.200
|
0.80
|
15.0
|
1.79
|
8
|
0.200
|
1.00
|
15.0
|
2.01
|
9
|
0.200
|
1.20
|
15.0
|
2.19
|
10
|
0.200
|
0.40
|
10.0
|
1.27
|
11
|
0.200
|
0.40
|
20.0
|
1.29
|
12
|
0.200
|
0.40
|
25.0
|
1.25
|
13
|
0.200
|
0.40
|
30.0
|
1.26
|
In trials 1 through 5, the
mass of the bob was systematically altered while keeping the other quantities
constant. By so doing, the experimenters were able to investigate the possible
effect of the mass upon the period. As can be seen in these five trials,
alterations in mass have little effect upon the period of the pendulum.
In trials 4 and 6-9, the mass is held constant at
0.200 kg and the arc angle is held constant at 15°. However, the length of the
pendulum is varied. By so doing, the experimenters were able to investigate the
possible effect of the length of the string upon the period. As can be seen in
these five trials, alterations in length definitely have an effect upon the
period of the pendulum. As the string is lengthened, the period of the pendulum
is increased. There is a direct relationship between the period and the length.
Finally, the experimenters investigated the
possible effect of the arc angle upon the period in trials 4 and 10-13. The
mass is held constant at 0.200 kg and the string length is held constant at
0.400 m. As can be seen from these five trials, alterations in the arc angle
have little to no effect upon the period of the pendulum.
CONCLUSION
So the conclusion from such an
experiment is that the one variable that effects the period of the pendulum is
the length of the string. Increases in the length lead to increases in the
period
For Procedures, See your Mechanical Laboratory Manual.
Please
Do Not Use This Reference Material WORD FOR WORD View Terms Of usage policy Page of this site for more Info on how to use this site
Observations :-
1.
Applications:-
1.
PRECAUTIONS:
For
Precautions, See General Laboratory Precautions
Please
Do Not Use This Reference Material WORD FOR WORD View Terms Of usage policy Page of this site for more Info on how to use this site.





Blogger Comment
Facebook Comment