Please Do Not Use This
Reference Material WORD FOR WORD View Terms Of usage policy Page of this
site for more Info on how to use this site
Title: The Single Phase Transformer
Aim: To verify that the voltage ratio between
the primary voltage and secondary voltage of a transformer is equal in turns
with the winding ratio, and to study the characteristics of a transformer on
No-Load and on Load
Apparatus:
(See
Apparatus in your Lab Manual on page 25)
Please Do Not Use This
Reference Material WORD FOR WORD View Terms Of usage policy Page of this
site for more Info on how to use this site
THEORY:
The single-phase transformer is used,
above all, in mains power units for supplying different types of electrical
equipment. The transformer is then used to change the mains voltage to other
voltages that are required in the equipment.
The single-phase transformer consists of two windings on
a common iron core. If one of the windings is connected to an AC voltage V1, an
alternating magnetic field will be set up in the iron core. This field will
then induce an AC voltage V2 in the other winding.
The ratio between these voltages is the same as the ratio
between the number of turns on the two windings:
V1/V2=N1/N2
The winding for the higher voltage is called the up
winding and the other winding is called the down winding.
If the transformer is connected in an electric circuit
the input winding is called the primary winding.
The other winding, which gives out power, is called the
secondary winding.
In reality the up and down windings of a transformer are
wound on top of each other, and not side by side as shown in the figure. This
arrangement results in reduced leakage magnetic flux, and thus a smaller
voltage drop in the transformer on load. In transformer MV 1911, however, the
windings are laid side by side so that a larger, and hence easier to measure, voltage
drop is obtained in the transformer when carrying out the laboratory exercises.
Transformer on No-Load
Let us consider one electrical transformer with only core
losses, which means, it has only core losses but no copper loss and no leakage
reactance of transformer. When an alternating source is applied in the primary,
the source will supply the current for magnetizing the core of transformer. But
this current is not the actual magnetizing current, it is little bit greater
than actual magnetizing current.
Actually, total current supplied from
the source has two components, one is magnetizing current which is merely
utilized for magnetizing the core and other component of the source current is
consumed for compensating the core losses in transformer. Because of this core
loss component, the source current in transformer on no-load condition supplied
from the source as source current is not exactly at 90° lags of supply voltage,
but it lags behind an angle θ is less than 90°. If total current supplied from
source is Io, it will have one component in phase with supply voltage V1 and
this component of the current Iw is core loss component. This component is
taken in phase with source voltage, because it is associated with active or
working losses in transformer. Other component of the source current is denoted
as Iμ.
This component produces the alternating
magnetic flux in the core, so it is watt-less; means it is reactive part of the
transformer source current.
Hence Iμ will be in quadrature with V1 and in phase with
alternating flux Φ.
Hence, total primary current in transformer on no-load
condition can be represented as
Now you have seen how simple is to explain the theory of
transformer in no-load.
Transformer On-Load
Theory of Transformer On Load But Having No Winding
Resistance and Leakage Reactance
Now we will examine the behavior of
above said transformer on load, that means load is connected to the secondary
terminals. Consider, transformer having core loss but no copper loss and
leakage reactance. Whenever load is connected to the secondary winding, load
current will start to flow through the load as well as secondary winding.
This load current solely depends upon
the characteristics of the load and also upon secondary voltage of the
transformer. This current is called secondary current or load current, here it
is denoted as I2. As I2 is flowing through the secondary, a self mmf in
secondary winding will be produced. Here it is N2I2, where, N2 is the number of
turns of the secondary winding of transformer.
This mmf or magneto motive force in the secondary winding
produces flux φ2. This φ2 will oppose the main magnetizing flux and momentarily
weakens the main flux and tries to reduce primary self induced emf E1. If E1
falls down below the primary source voltage V1, there will be an extra current
flowing from source to primary winding. This extra primary current I2′ produces
extra flux φ′ in the core which will neutralize the secondary counter flux φ2.
Hence the main magnetizing flux of core, Φ remains unchanged irrespective of
load.
So total current, this transformer draws
from source can be divided into two components, first one is utilized for
magnetizing the core and compensating the core loss i.e. Io. It is no-load
component of the primary current. Second one is utilized for compensating the
counter flux of the secondary winding. It is known as load component of the
primary current.
Hence total no load primary current I1 of a electrical
power transformer having no winding resistance and leakage reactance can be
represented as follows
Where θ2 is the angle between Secondary
Voltage and Secondary Current of transformer.
Now we will proceed one further step
toward more practical aspect of a transformer.
Theory of Transformer On Load, With Resistive Winding,
But No Leakage Reactances
Now, consider the winding resistance of
transformer but no leakage reactance. So far we have discussed about the
transformer which has ideal windings, means winding with no resistance and
leakage reactance, but now we will consider one transformer which has internal
resistance in the winding but no leakage reactance. As the windings are resistive,
there would be a voltage drop in the windings.
We have proved earlier that, total
primary current from the source on load is I1. The voltage drop in the primary
winding with resistance, R1 is R1I1. Obviously, induced emf across primary
winding E1, is not exactly equal to source voltage V1. E1 is less than V1 by
voltage drop I1R1.
Again in the case of secondary, the voltage induced
across the secondary winding, E2 does not totally appear across the load since
it also drops by an amount I2R2, where R2 is the secondary winding resistance
and I2 is secondary current or load current.
Theory of Transformer On Load, With Resistance As Well As
Leakage Reactance in Transformer Windings
Now we will consider the condition, when
there is leakage reactance of transformer as well as winding resistance of
transformer.
Let leakage reactances of primary and
secondary windings of the transformer are X1 and X2 respectively.
Hence total impedance of primary and secondary winding of
transformer with resistance R1 and R2 respectively, can be represented as,
We have already established the voltage
equation of a transformer on load, with only resistances in the windings, where
voltage drops in the windings occur only due to resistive voltage drop. But
when we consider leakage reactances of transformer windings, voltage drop
occurs in the winding not only because of resistance, it is because of
impedance of transformer windings. Hence, actual voltage equation of a
transformer can easily be determined by just replacing resistances R1 & R2
in the previously established voltage equations by Z1 and Z2.
Therefore, the voltage equations are,
Resistance drops are in the direction of current vector
but, reactive drop will be perpendicular to the current vector as shown in the
above vector diagram of transformer.
For
Procedure, See your Electrical Laboratory Manual on pages 25, 26 and 27.
Fill Up
Tables in Your Manual and Continue To….
PRECAUTIONS:
For
Precautions, See General Electrical Lab
Precautions
Answers
to Questions:
1. Copper losses result from Joule
heating and so are also referred
to as "I squared R losses", in reference to Joule's First Law. This states that
the energy lost eachsecond, or power,
increases as the square of the current through the windings
and in proportion to the electrical resistance of the conductors.
where I is the current
flowing in the conductor and R the resistance of the conductor. With I in amperes and R in ohms, the calculated power
loss is given in watts.
2. Copper Losses can be
determined by the product of the square of current and the resistance the copper
= I2.R
Please Do Not Use This
Reference Material WORD FOR WORD View Terms Of usage policy Page of this
site for more Info on how to use this site





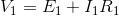




Blogger Comment
Facebook Comment